ホーム
>>
RSSセンター
>>
苦しまぎれの旋回理論 その2
飛行中年
(2024/12/25 18:57:24)
苦しまぎれの旋回理論 その2
(2015/7/1 22:57:01)
RSSセンター
| メイン | 簡易ヘッドライン |
飛行中年
(2024/12/25 18:57:24)
苦しまぎれの旋回理論 その2
(2015/7/1 22:57:01)
ハンググライダーはなぜ旋回出来るのか？
舵も何もついていないハンググライダーが空を思うがままに飛べるその理由を知ることは、一見とても簡単そうに思えるのですが、実はハン
ググライダーは舵がないからこそその旋回の理論の説明は難しく、いままで誰も満足にそれが出来た人はいませんでした。
これは具体的にどういったことから説明出来ないのか？について、前回では過去に言われていたフラッター説、ビローシフト説の矛盾点につい
てご説明しました。
そして今回…。
もう一つ唱えられているハンググライダーの旋回理論の「後退角説」をご説明しますが、実はこの説でさえも矛盾点があるのです…。
「後退角」とは翼が後ろに後退した翼のこと…。
翼が後ろに後退していると、「風見鶏効果」が生まれます。
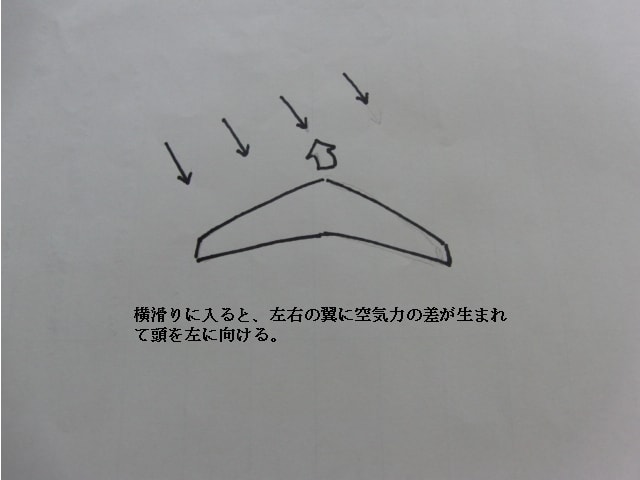
上の図を見ていただければ分かりますが、後退角を持つ翼に偏った方向から風が入ると、その左右の翼に当たる空気力の差により、翼は風が来
る方向に向きを変えようとします。
風がくる方向に常に向きたがるので、これを風見鶏効果と呼んでいるのです。
ハンググライダーにはもちろん後退角がありますが、体重移動により傾いた機体は、その傾いた方向に横滑りをするため、風見鶏効果でそちら
に向きを変える…。
つまり旋回出来る！
これがハンググライダーの旋回を説明する後退角説なのです!
この説、一見理にかなっているようなのですが…。
実はどうしても腑に落ちない点がいくつかあるのです‥。
まず一番目‥。
風見鶏効果は空気の力で現れるわけですから、空気力が強くなるほど、つまり、速度が速くなるほど横滑りした方にその向きを変えたがるはずです！
しかし‥。
実際のハングの動きを観察してみると、これの反対！！ つまり、速度が速いほど向きを変えるのに時間がかかり、低速の旋回の方がなぜか強くノーズの向きを変える力が出ているのです‥。
これは、初心者が初級機で速度不足のままランディング前の高度処理をしているのを見ればよく分かるのですが、ハングは旋回時ほんの少し横滑りしたかな？と、思った次の瞬間、クルッと向きを変えてしまいます！
この旋回を見ると、どうしても後退角説による旋回の説明に疑問がわいてしまうんです‥。
二番目‥。
一昔前、ウイングレットというものが流行りました！
翼端についているアレ！ですが、最近ではカーブドチップが主流なので見かけなくなりましたね。
このウイングレット。装着して飛んでみると不思議なことが起こるんです‥。
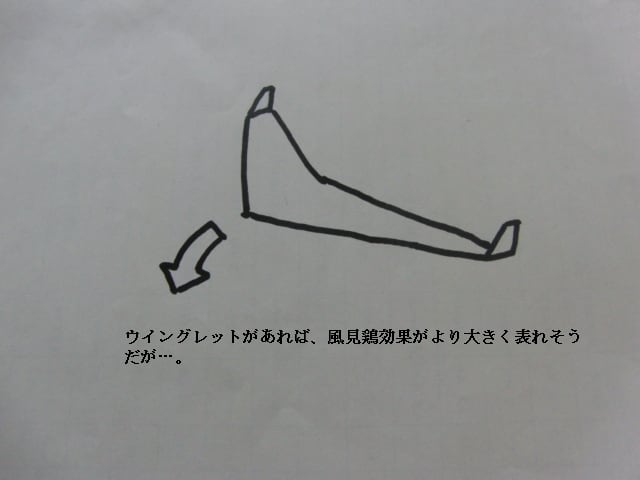
風見鶏効果でハングが旋回しているのであれば、重心位置よりはるか後ろに垂直尾翼のようなウイングレットがあれば、より風見鶏効果が強く表れて旋回がスムーズになるはずなのですが‥。
実際には反対なのです！
ウイングレットを装着すると、旋回が若干ですが遅れてしまうんです‥。
この傾向はどのハンググライダーにウイングレットを装着しても結果は同じ‥。
感じとしてはせっかくハングが向きを変えたがっているのに、それをウイングレットが束縛しているような感覚なんです‥。
トドメに三番目‥。
過去多くの方がハンググライダーの旋回理論を解き明かすために、模型を作ってその重心位置を横にずらして飛ばしてみました。
この模型はもちろんちゃんと飛ぶようにねじり下げもついていますが、ビローはありません。
で、この模型を飛ばしてみると‥。
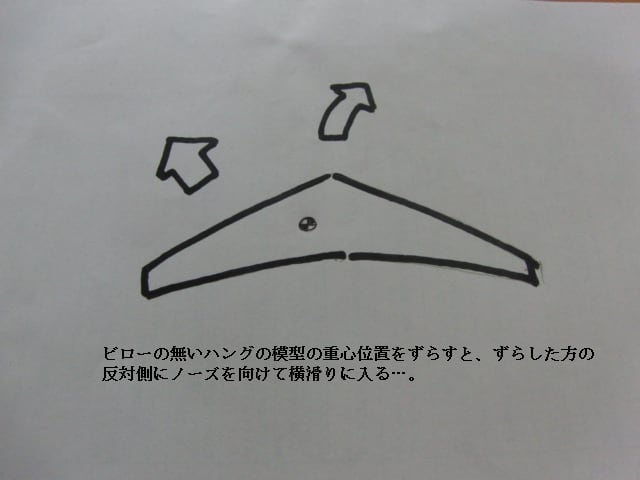
重心をずらした方と反対側にノーズを向けて、そして、横滑りに入ってしまうのです！
ちょっとあのスムーズなハングの旋回とはイメージがつながりません‥。
この理由は分かっています！
支えのない物体に外力が加わると、その物体は重心位置を中心に回転運動をしようとします。
重心がずらされたハングの模型は、重心を中心に考えれば上の図の場合、右側の方が空気力が大きくなります。
つまり、右の方が抵抗が大きくなるのです！
その結果、ハングの模型は右に向いてしまうのです‥。
過去、ハンググライダーの旋回に疑問を持ち、そしてその理由を解き明かそうとした方たちは、この辺で何がなんだかわからなくなりサジを投げてしまっていたんです。
私もやはり同じようにここから先に進めずにいたのですが‥。
１０年ほど前のことです。昔「FLYAIR」という雑誌があったのですが、この編集長をしているNヶ谷さんに一連のこの話をしたところ‥。
「面白い！どうです！！ハングの旋回の理論を調べるための企画を雑誌で立ててみませんか？ スタッフと機材はこちらで提供します！」
とういうことになって、本格的にこの問題について取り組めるチャンスをいただいたことがあったんです。
その結果、実は摩訶不思議な現象を発見し、私はその現象をヒントに今までにない全く新しいハンググライダーの旋回理論を思いついたのです！
それについては次回！
舵も何もついていないハンググライダーが空を思うがままに飛べるその理由を知ることは、一見とても簡単そうに思えるのですが、実はハン
ググライダーは舵がないからこそその旋回の理論の説明は難しく、いままで誰も満足にそれが出来た人はいませんでした。
これは具体的にどういったことから説明出来ないのか？について、前回では過去に言われていたフラッター説、ビローシフト説の矛盾点につい
てご説明しました。
そして今回…。
もう一つ唱えられているハンググライダーの旋回理論の「後退角説」をご説明しますが、実はこの説でさえも矛盾点があるのです…。
「後退角」とは翼が後ろに後退した翼のこと…。
翼が後ろに後退していると、「風見鶏効果」が生まれます。
上の図を見ていただければ分かりますが、後退角を持つ翼に偏った方向から風が入ると、その左右の翼に当たる空気力の差により、翼は風が来
る方向に向きを変えようとします。
風がくる方向に常に向きたがるので、これを風見鶏効果と呼んでいるのです。
ハンググライダーにはもちろん後退角がありますが、体重移動により傾いた機体は、その傾いた方向に横滑りをするため、風見鶏効果でそちら
に向きを変える…。
つまり旋回出来る！
これがハンググライダーの旋回を説明する後退角説なのです!
この説、一見理にかなっているようなのですが…。
実はどうしても腑に落ちない点がいくつかあるのです‥。
まず一番目‥。
風見鶏効果は空気の力で現れるわけですから、空気力が強くなるほど、つまり、速度が速くなるほど横滑りした方にその向きを変えたがるはずです！
しかし‥。
実際のハングの動きを観察してみると、これの反対！！ つまり、速度が速いほど向きを変えるのに時間がかかり、低速の旋回の方がなぜか強くノーズの向きを変える力が出ているのです‥。
これは、初心者が初級機で速度不足のままランディング前の高度処理をしているのを見ればよく分かるのですが、ハングは旋回時ほんの少し横滑りしたかな？と、思った次の瞬間、クルッと向きを変えてしまいます！
この旋回を見ると、どうしても後退角説による旋回の説明に疑問がわいてしまうんです‥。
二番目‥。
一昔前、ウイングレットというものが流行りました！
翼端についているアレ！ですが、最近ではカーブドチップが主流なので見かけなくなりましたね。
このウイングレット。装着して飛んでみると不思議なことが起こるんです‥。
風見鶏効果でハングが旋回しているのであれば、重心位置よりはるか後ろに垂直尾翼のようなウイングレットがあれば、より風見鶏効果が強く表れて旋回がスムーズになるはずなのですが‥。
実際には反対なのです！
ウイングレットを装着すると、旋回が若干ですが遅れてしまうんです‥。
この傾向はどのハンググライダーにウイングレットを装着しても結果は同じ‥。
感じとしてはせっかくハングが向きを変えたがっているのに、それをウイングレットが束縛しているような感覚なんです‥。
トドメに三番目‥。
過去多くの方がハンググライダーの旋回理論を解き明かすために、模型を作ってその重心位置を横にずらして飛ばしてみました。
この模型はもちろんちゃんと飛ぶようにねじり下げもついていますが、ビローはありません。
で、この模型を飛ばしてみると‥。
重心をずらした方と反対側にノーズを向けて、そして、横滑りに入ってしまうのです！
ちょっとあのスムーズなハングの旋回とはイメージがつながりません‥。
この理由は分かっています！
支えのない物体に外力が加わると、その物体は重心位置を中心に回転運動をしようとします。
重心がずらされたハングの模型は、重心を中心に考えれば上の図の場合、右側の方が空気力が大きくなります。
つまり、右の方が抵抗が大きくなるのです！
その結果、ハングの模型は右に向いてしまうのです‥。
過去、ハンググライダーの旋回に疑問を持ち、そしてその理由を解き明かそうとした方たちは、この辺で何がなんだかわからなくなりサジを投げてしまっていたんです。
私もやはり同じようにここから先に進めずにいたのですが‥。
１０年ほど前のことです。昔「FLYAIR」という雑誌があったのですが、この編集長をしているNヶ谷さんに一連のこの話をしたところ‥。
「面白い！どうです！！ハングの旋回の理論を調べるための企画を雑誌で立ててみませんか？ スタッフと機材はこちらで提供します！」
とういうことになって、本格的にこの問題について取り組めるチャンスをいただいたことがあったんです。
その結果、実は摩訶不思議な現象を発見し、私はその現象をヒントに今までにない全く新しいハンググライダーの旋回理論を思いついたのです！
それについては次回！
execution time : 0.007 sec